Le non-paradoxe du conducteur distrait

Léo Gerville-Réache  – IMB – UMR 5251 – Université de Bordeaux

Résumé : Le paradoxe du conducteur distrait (Absent-Minded Driver Paradox) est un paradoxe récent. Apparu en 1994 dans un document de travail de Michele Piccione et Ariel Rubinstein, il n’a produit jusqu’ici que relativement peu de littérature. En réalité, il semble qu’il se soit rapidement scindé en deux. D’une part, le paradoxe original posant la question de l’inconstance d’une stratégie a priori optimale qui, au moment d’être mise en œuvre, ne le serait plus. D’autre part, la question de l’établissement d’un degré de croyance rationnelle dans une expérience de pensée avec incident cognitif. Cet article, le premier en langue française, revient sur ce problème et propose une remise en cause de l’équation à l’origine du « paradoxe ».

1) Introduction

Le paradoxe du conducteur distrait est un paradoxe récent de théorie des jeux. Proposé par Michele Piccione et Ariel Rubinstein dans un document de travail en 1994, il est publié dans un numéro spécial de la revue Games and economic behavior en 1997. Dans le même journal, une dizaine d’articles sur le sujet sont publiés dont deux écrits par Robert Aumann, Sergiu Hart et Motty Perry, tentant de clore le débat.

Le paradoxe

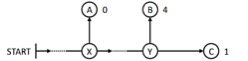
Après une soirée arrosée, vous devez rentrer chez vous. A la sortie du Bar (Start), vous savez que votre maison est à la deuxième intersection à gauche (B). Vu votre état, vous savez qu’une fois arrivé à un carrefour, vous serez incapable de vous situer, c’est-à-dire que vous ne saurez pas si vous êtes au premier ou au deuxième carrefour…

Si au premier carrefour (X), vous tournez à gauche, vous arriverez en (A) et gagnerez zéro, si vous allez jusqu’au deuxième carrefour (Y) et tournez à gauche, vous arriverez en (B) et gagnerez 4. Enfin, si vous allez toujours tout droit, vous arriverez en (C) et gagnerez 1.

Quelle stratégie maximisera votre espérance de gain ? Cette stratégie construite à la sortie du bar sera-t-elle encore valable une fois arrivé à un carrefour ?

A la sortie du bar, vous cherchez une stratégie. Celle-ci devra nécessairement être la même à chaque carrefour que vous atteindrez effectivement. En effet, ne pouvant distinguer les carrefours, vous ne pourrez pas adapter votre stratégie en fonction du carrefour. Aussi, vous cherchez une stratégie du type : « A chaque carrefour, je continue tout droit avec probabilité p et je tourne à gauche avec probabilité 1-p. » Aussi votre espérance de gain à la sortie du bar vaut :

Cette espérance est maximale pour p=2/3 et vaut alors 4/3. Aussi, avant de partir du bar, vous planifiez qu’à chaque carrefour vous lancerez un dé et s’il tombe sur 1 ou 2, vous tournez à gauche, sinon, vous continuez tout droit. Soit…

Maintenant vous êtes à un carrefour, incapable de savoir si ce carrefour est le premier (X) ou le deuxième (Y). Vous vous préparez à lancer votre dé mais vous vous dites :

Je ne sais pas si je suis en X ou en Y mais je ne peux pas être certain d’être en X. Aussi,

– Si je suis en X, mon espérance de gain est :

– Si je suis en Y, mon espérance de gain est :

En notant q la probabilité (croyance), étant à un carrefour, d’être au premier carrefour (X), mon espérance de gain « au carrefour » est donc :

Mais pour p=2/3, E_carrefour=2-2q/3 et, sauf pour q=1, E_carrefour est strictement supérieure à 4/3. Aussi, en excluant la certitude d’être au premier carrefour, il n’est plus optimal de prendre mon dé et d’appliquer la stratégie que j’avais mise au point à la sortie du bar. Etant à ce carrefour, soit je crois avec probabilité q=1 que je suis en X et je dois appliquer la stratégie p=2/3, soit je crois qu’il est possible que je sois en Y (probabilité 1-q>0) et il faut que je reconsidère ma stratégie car sinon je ne maximise plus, ici et maintenant, mon espérance de gain !

Alors… une fois au carrefour, que devez-vous croire, que devez-vous faire ?

Un paradoxe non résolu

En fin du numéro spécial de la revue Games and economic behavior, Michele Piccione et Ariel Rubinstein répondent aux différentes analyses proposées en rappelant d’abord leurs intentions :

Les questions que nous avons soulevées peuvent être résumées par les questions suivantes :

1. Quelles décisions peuvent être prises ? En particulier, un agent peut-il décider du moment où prendre une décision ?

2. Quel est le déroulement temporel des décisions ? Y a-t-il une planification possible ou bien les décisions sont prises uniquement au moment où les actions sont exécutées ?

3. Un agent peut-il changer sa stratégie au long de son exécution ? Et, s’il change sa stratégie, peut-il en changer à nouveau ?

4. Un agent peut-il utiliser des dispositifs aléatoires ?

Les auteurs conclurent ainsi :

Malgré tout ce qui a été dit, nous sommes encore confus à propos de sa résolution […] Les problèmes de décision tels que l’exemple de conducteur peuvent être analysés raisonnablement de plusieurs façons. En tant que théoriciens, nous pouvons tout au plus préciser la part de logique de chacune de ces analyses.

Depuis 1997, et encore très récemment (en 2014), plusieurs chercheurs (par exemple : Jean Baratgin et Bernard Walliser, Kenneth Binmore, Steven Landsburg, Wolfgang Schwarz,…) poursuivent les tentatives de résolution. Souvent consignées dans des documents de travail, leurs analyses nous laissent, aujourd’hui encore, sans réponse consensuelle. Cet article présente le paradoxe et brièvement les questions qu’il soulève. Enfin, est développé un point de vue original sur une possible erreur dans la formule même de l’espérance de gain au carrefour, source du paradoxe.

2) Newcomb et la Belle au bois dormant

Il semble que ce paradoxe pose des questions bien délicates. Certaines font penser au paradoxe de Newcomb (Itzhak Gilboa , Wolfgang Schwarz) alors que d’autres font l’objet du paradoxe de la Belle au bois dormant (en particulier, Jean Baratgin et Bernard Walliser, Wolfgang Schwarz).

Le paradoxe de Newcomb

Ce problème toujours ouvert de théorie des jeux a été introduit par Robert Nozick en 1969. Il pose une question de décision rationnelle et interroge l’axiomatique de Von Neumann et Morgenstern. Plus important ici, il interroge également sur la temporalité, la destinée et in fine, le libre arbitre.

La fée annonce: (1) Je ne me trompe jamais dans mes prédictions; (2) Voici une boîte rouge et une boîte bleue; (3) Tu pourras ouvrir soit la boîte bleue, soit la boîte rouge et la boîte bleue, et tu prendras alors le contenu des boîtes ouvertes; (4) Dans la boîte rouge, je mettrai 100 euros; (5) Avant de remplir la boîte bleue, je ferai une prédiction (que je ne te communiquerai pas) :

– Si je prédis que tu prendras la boîte bleue toute seule, je mettrai 1000 euros à l’intérieur ;

– Si je prédis que tu prendras les deux boîtes, je ne mettrai rien dans la boîte bleue.

Premier raisonnement :

– Si la prédiction a été que je ne prendrai que la boite bleue, alors prendre les deux boîtes rapporte 1100 €, alors que ne prendre que la boîte bleue ne rapporte que 1000 €.

– Si la prédiction a été que je prendrai les deux boîtes, alors prendre les deux boîtes rapporte 100 €, et prendre juste la boîte bleue rapporte 0 €.

Il est donc clair qu’il faut prendre les deux boîtes.

Second raisonnement:

– Si je prends les deux boîtes, comme cela aura été prévu par la fée, il y aura 0€ dans la boite bleue et mon gain total sera de 100€.

– Si je ne prends que la boîte bleue, comme cela aura été prévu par la fée, il y aura 1000€ dans la boîte bleue et mon gain total sera de 1000€.

Il est donc clair qu’il faut prendre seulement la boîte bleue.

Le premier raisonnement est basé sur l’élimination des stratégies fortement dominées (une fois les sommes mises dans les boîtes, ne prendre que la boîte bleue est toujours moins payant que de prendre les deux boîtes) alors que le second se base sur la maximisation de l’utilité espérée (en ne prenant que la boîte bleue, mon gain sera de 1000 euros alors qu’en prenant les deux boîtes, mon gain ne sera que de 100 euros). Mais, il y a possiblement une contradiction dans l’énoncé. Les propositions (1) et (3) seraient incompatibles. En effet si j’ai le « choix » alors la fée peut se tromper (i.e. (3) → non(1)). Si la fée ne se trompe jamais, alors je n’ai pas le « choix » (i.e. (1) → non(3)). Cette question du choix possible ou impossible constitue l’une des problématiques du conducteur distrait (voir par exemple Itzhak Gilboa 1997).

Le point particulièrement délicat du raisonnement fait au carrefour est que la croyance q d’être au carrefour X dépend de la probabilité p de la stratégie établie à la sortie du bar. Pour bien voir cela, considérons la croyance 1-q que le carrefour où je me trouve effectivement au moment de mon raisonnement soit Y. Pour être en Y, il faut avoir été en X et qu’en X j’ai appliqué une stratégie qui m’a conduit à Y avec une certaine probabilité strictement positive. Aussi, 1-q dépend nécessairement d’une stratégie déjà mise en place et utilisée en X. Mais alors, comment est-il possible d’appliquer en Y une autre stratégie que celle que j’ai déjà appliquée en X? En effet, nous avons convenu précédemment que, comme les carrefours sont indiscernables, la stratégie ne peut être différente d’un carrefour à « l’autre ».

L’équation de l’espérance de gain au carrefour n’aurait pas de solution. L’idée de construire une stratégie étant au carrefour produirait une sorte de référence temporelle circulaire comme si l’on pouvait agir sur une stratégie possiblement déjà mise en place dans le passé. En effet, une fois à un carrefour, je suis contraint d’admettre qu’une stratégie a peut-être déjà été utilisée et que c’est alors nécessairement la même que je dois réitérer maintenant. Laquelle, si ce n’est celle que j’ai planifiée à la sortie du bar (je ne peux me souvenir d’aucune autre) ? Aussi, je n’aurai en réalité plus le choix. Je dois m’en tenir à ma stratégie initiale car c’est la seule qui est rationnellement justifiable et constante d’un carrefour à « l’autre ».

Imaginer, une fois au carrefour, que l’on aurait la possibilité de changer de stratégie et de ne pas appliquer p=2/3, c’est rendre impossible l’établissement d’une croyance rationnelle d’être en X comme d’être en Y. L’espérance de gain au carrefour (E_carrefour=(1+pq–q)(4-3p)), n’a pas de solution optimale rationalisable. On est alors dans un dilemme rationnel qui nous oblige à agir au carrefour comme on l’avait défini à la sortie du bar alors même que l’on ne considère plus cette stratégie comme optimale au moment précis de la mettre en œuvre.

Le paradoxe de la Belle au bois dormant

Ce problème toujours ouvert, proposé par Adam Elga en 2000 est un problème d’auto-localisation après un incident cognitif qui oppose en particulier deux raisonnements : l’un est dit « demiste » et l’autre « tiériste ».

Le dimanche soir des chercheurs se préparent à vous endormir. Pendant les deux jours que durera votre sommeil ils vous réveilleront brièvement soit une soit deux fois, selon le résultat d’un unique lancer d’une pièce équilibrée (si Face, un réveil lundi ; si Pile, un réveil lundi et un mardi). Après chaque réveil, ils vous endormiront à nouveau à l’aide d’une drogue qui vous fera oublier ce dernier réveil.

Lorsque vous êtes réveillé, à quel degré devez-vous croire que le résultat du lancer de la pièce de monnaie est Face?

Les deux raisonnements qui s’opposent sont résumés ainsi par Laurent Delabre (2015):

Le premier raisonnement, typiquement bayésien, travaille une probabilité épistémique introduite dès le départ par alignement sur des chances objectives, en l’occurrence la propension de la pièce à tomber du côté face : quand la Belle se réveille dans l’expérience, elle maintient son degré de croyance en face du dimanche parce qu’elle respecte un principe d’inertie doxastique (pas d’information nouvelle pertinente, pas de révision des croyances).

Le second raisonnement, fréquentiste, opte pour une « lecture ontologique fictionnelle » de la probabilité cherchée : la Belle se rappelle le protocole, imagine que l’expérience est répétée, que son réveil est un réveil parmi des milliers, et juge par conséquent qu’elle a deux fois plus de chances de vivre un réveil-pile ; elle ne conclut un degré de croyance, calqué sur la fréquence des réveils-face, que parce que la question de l’entretien l’exige.

Le premier argument conclut 1/2, le second mène à 1/3.

Pour notre conducteur distrait, peut-on alors raisonner, à la sortie du bar, en intégrant le fait que l’on pourrait se retrouver dans un dilemme du type de celui de la Belle au bois dormant au moment d’agir au carrefour ?

« Je sais déjà qu’une fois arrivé à un carrefour je ne considérerai plus comme optimale la solution p=2/3. Je sais également que je ne pourrai appliquer que la stratégie que je vais mettre en place maintenant (à la sortie du bar) car aucune modification une fois au carrefour ne serait rationalisable. Enfin, cette stratégie est nécessairement la même quel que soit le carrefour où je me trouverai. Puis-je alors tenir compte de tout cela dans la stratégie que je vais mettre en place à la sortie du bar ? »

Il semble qu’un tel raisonnement soit possible. A la sortie du bar, il ne faut pas maximiser E_bar=p(4-3p) mais maximiser :

Mais attention, le problème est alors d’exprimer q en fonction de p. En effet, nous avons déjà vu que q et p sont intimement liés. Selon Wolfgang Schwarz (2014), deux thèses s’affrontent alors : ce sont bien les thèses tiériste et demiste du paradoxe de la Belle au dois dormant :

– les tiéristes diront que q=1(1+p),

– les demistes diront que q=1-p/2.

Cela produira alors deux stratégies distinctes :

– pour un tiériste, le maximum de E_carrefour est alors atteint pour p≈0,53 ; la croyance d’être en X vaut alors q≈0,65 ; l’espérance de gain à la sortie du bar vaut E_bar≈1,28 ; l’espérance de gain au carrefour vaut E_carrefour≈1,67,

– pour un demiste, le maximum de E_carrefour est atteint pour p≈0,58 ; la croyance d’être en X vaut alors q≈0,71 ; l’espérance de gain à la sortie du bar vaut E_bar≈1,31 ; l’espérance de gain au carrefour vaut E_carrefour≈1,59.

Aussi, que l’on soit demiste ou tiériste, il existe une stratégie propre qui, à chaque moment où elle sera appliquée, laisserait le conducteur distrait dans un état de croyance en accord avec l’optimalité de sa stratégie. En partant du bar, il sait que cette stratégie n’est pas optimale mais il sait qu’il la croira optimale au moment de la mettre effectivement en œuvre.

N’est-ce pas cela la rationalité d’une action ; une action serait rationnelle si elle est justifiable au moment effectif de sa mise en œuvre ?

Il est cependant important de préciser le sens de l’espérance au carrefour (E_carrefour) par rapport à celle au bar (E_bar). En faisant appel à l’argument de la répétition de l’expérience, l’espérance au bar exprime bien le fait « qu’en moyenne » je gagnerai E_bar. En revanche, l’espérance de gain au carrefour ne signifie aucunement « qu’en moyenne », en cas ce répétition, je gagnerai  E_carrefour. Ici l’espérance de gain au carrefour est épistémique, pas ontique. C’est-à-dire qu’elle est construite sur l’injection de croyances (demistes ou tiéristes, peu importe) d’être en X ou en Y dans une équation générique d’espérance de gain au carrefour et pas sur l’injection de probabilités objectives, conformes (en particulier) à l’interprétation fréquentiste du concept de probabilité et d’espérance.

Mais alors, que doit-on faire ? Peut-on suivre une stratégie, issue d’une croyance au carrefour, qui produira une espérance de gain épistémique supérieure à 4/3, alors même que l’espérance de gain ontique (« en moyenne ») sera inférieure à ce même 4/3 ?

3) Et si la solution était ailleurs ?

Reprenons l’expression à l’origine du paradoxe :

On considère que l’on est ici en capacité de calculer l’espérance de gain au carrefour comme la somme du produit des croyances d’être en X (resp. en Y) par les espérances de gain conditionnelles aux hypothèses d’être en X (resp. en Y). Il est clair qu’au carrefour, je suis soit en X, soit en Y. Il est également clair que ma croyance d’être X ajoutée à celle d’être en Y doit faire un. Cependant, pour « être en Y« , il aura fallu, auparavant, « être en X« . Il semble qu’une part de cette espérance au carrefour soit possiblement redondante, ou encore inadmissible.

Est-il possible que la formule de l’espérance de gain au carrefour proposée par Michele Piccione et Ariel Rubinstein et acceptée par tous les auteurs sur le sujet soit simplement fausse ?

Avant d’explorer cette question, tentons dans un premier temps de raisonner conditionnellement à l’hypothèse de se trouver au carrefour final.

– Soit le carrefour où je me trouve est X et c’est le carrefour final, cela se produit avec probabilité 1-p (avec un gain de 0) et donc :

– Soit le carrefour où je me trouve est Y (Y est nécessairement un carrefour final), cela se produit avec probabilité p, avec un gain espéré de E_Y =4-3p.

L’espérance de gain au carrefour serait alors :

On se demande alors où est passée la possibilité que le carrefour où je me trouve soit X et que ce carrefour ne soit pas le carrefour final. Mais cette possibilité qui consiste à dire que l’on arrivera effectivement en Y est déjà prise en compte dans E_Y. Aussi, la question ne serait pas de savoir dans quelle mesure je dois croire que je suis au carrefour X ou Y. La question serait de savoir dans quelle mesure je dois croire que je suis au carrefour final X ou en Y.

Ce raisonnement conduit à dire que l’espérance de gain au carrefour, peut se décomposer aisément conditionnellement au carrefour final. Cette espérance, est alors la même que celle à la sortie du bar. L’action optimale au carrefour est alors bien de continuer tout droit avec probabilité p=2/3. Il n’y aurait donc aucun dilemme rationnel et seulement une écriture erronée de l’espérance de gain au carrefour. L’espérance de gain au carrefour décomposée via les croyances au carrefour d’être X et Y, telle que proposée par Piccione et Rubinstein, serait finalement fausse.

Pour autant, on resterait sur notre fin en admettant une sorte d’impossibilité à décomposer l’espérance de gain au bar en une somme pondérée d’espérances conditionnelles aux hypothèses d’être en X ou en Y. L’écriture correcte pourrait être en réalité la suivante :

Cette formule tient compte du fait que la contribution au calcul de l’espérance de gain au carrefour, de la part conditionnelle à l’hypothèse d’être en Y (i.e. E_Y), doit intégrer que l’on ne peut pas croire être en Y et déjà avoir tourné à gauche. Aussi, on doit retirer à l’espérance de gain E_Y, la part impossible correspondant au produit de la probabilité de finir en A par l’espérance de gain en Y (soit : (1-p)E_Y). Précisément, si je crois que je suis en Y, je ne peux pas inclure dans l’espérance associée, la possibilité d’avoir déjà tourné une fois à gauche auparavant. En effet la contribution « qE_Y » suppose possible (avec probabilité 1-p) que l’on tourne à gauche en X. Pourtant, de deux choses l’une : soit la contribution associée à la croyance d’être en Y est défalquée de la possibilité d’avoir pu déjà tourner à gauche (calcul de E^*_carrefour), soit on multiplie la part conditionnelle à l’hypothèse d’être en Y, par la probabilité de ne pas avoir encore tourné à gauche et on obtient l’équation de l’espérance au carrefour suivante :

En réalité, les deux raisonnements précédents tentent de traduire le fait spécifique que la probabilité d’une croyance effective au carrefour X n’est pas égale à la probabilité d’une croyance effective au carrefour Y. Nous nous devons alors de pondérer les contributions en X : qE_Y et en Y : (1-q)E_Y par les probabilités (ontiques) respectives de passer en X (qui vaut 1) et de passer en Y (qui vaut p). La construction adéquate de l’espérance de gain au carrefour serait, in fine, la suivante :

On peut remarquer que la question de la croyance d’être en X ou en Y ne participe plus au problème! Aussi, que l’on soit demiste ou tièriste n’est pas en question. Il est alors possible que le problème de la Belle au bois dormant, remarquable paradoxe, ait trouvé son origine dans une « simple » erreur ; celle faite dans la formulation de l’espérance de gain au carrefour, source du non-paradoxe du conducteur distrait. Pour autant, cette possible erreur et la correction qui est proposée pourraient bien trouver une place dans la réflexion sur ce qu’il conviendrait de croire au réveil dans le problème de la Belle au bois dormant.

4) Conclusion

Le paradoxe du conducteur distrait semble être un problème similaire à celui de Newcomb en lui ajoutant un problème d’auto-localisation repris depuis par le paradoxe de la Belle au bois dormant. C’est possible, et en matière de paradoxe, il convient d’être prudent. Pourtant, il semble bien que le problème vienne finalement d’une erreur dans la formulation même du paradoxe. L’équation de l’espérance de gain au carrefour proposée par Michele Piccione et Ariel Rubinstein ne prendrait pas en compte le fait que la probabilité d’une croyance effective au premier carrefour (X) n’est pas égale à la probabilité d’une croyance effective au deuxième carrefour (Y).

Bibliographie

Robert Aumann, Sergiu Hart, Motty Perry, The Absent-Minded Driver, Games and Econ. Behav. 20, 102-116, 1997.

Robert Aumann, Sergiu Hart, Motty Perry, The Forgetful Passenger, Games and Econ. Behav. 20, 117-120, 1997.

Jean Baratgin, Bernard Walliser, Sleeping Beauty and the absent-minded driver, Theory Dec., 69, 489-496, 2010.

Olivier Board, The not-so-absent-minded driver, Research in Economics 57, 189-200, 2003.

Laurent Delabre, Un jeune paradoxe : la Belle au bois dormant. Implications Philosophiques, https://www.implications-philosophiques.org/implications-epistemologiques/sciences/ paradoxes/belleauboisdormant/, 2015.

Adam Elga, Self-Locating Belief and the Sleeping Beauty Problem, Analysis 60, 143-147, 2000.

Itzhak Gilboa, A Comment on the Absent-Minded Driver Paradox, Games and Econ. Behav. 20, 25-30, 1997.

Robert Nozick, Newcomb’s problem and two principles of choice, in Essays in Honor of Carl G. Hempel, 1969.

Michele Piccione, Ariel Rubinstein, On the Interpretation of Decision Problems with Imperfect Recall, Games and Econ. Behav. 20, 3-24, 1997.

Michele Piccione, The Absent-Minded Driver’s Paradox: Synthesis and Responses, Games and Econ. Behav. 20, 121-130, 1997.

Wolfgang Schwarz, Lost memories and useless coins: Revisiting the absentminded driver, http://fitelson.org/few/few_12/schwarz_paper.pdf, 2014.